VAE的逻辑与实践

28 Jan 2018

引言
统计推断视角
神经网络视角
Reference

引言

变分自动解码器（VAE）是一个机器学习领域很重要的方法。关于这一方法实践上的操作并不复杂，和普通神经网络构成的编码解码器结构类似，编码器负责将高维的原始信息压缩降维成中间层的隐变量，解码器部分可以将低维的隐变量还原出尽可能接近原始信息的内容，最常见的对应，即是编码器类似图像识别，解码器类似图像生成。VAE 从神经网络的视角来看，和普通编码解码器非常相似。最多不过是训练时使用的损失函数加了一个类似正规化项的东西（KL散度），来强制使编码器产生的隐变量接近标准高斯分布，从而使得中间层的隐变量更加有代表性，隐变量间的距离也可以一定程度上代表原图片信息间的相似性，同时也使得指定低维隐变量生成新的图片成为可能。这些都是 VAE 相对于普通解码器的优点。

当然整个问题还可以完全从概率与统计推断的视角出发来论述，一旦这些概念用来描述 VAE 的相关结构，并和神经网络里的概念纠缠在一起，就很难理清楚整个逻辑链条。即使有参考文献里那些关于 VAE 深刻的认识和实践，在我读来，总觉得没有把所有的内容连成一条线。因此本文将从神经网络，概率统计两种视角，并直接结合代码分析 MNIST 数据集的具体例子，来阐述和 VAE 相关的大大小小的关键问题。

阅读本文，你需要对基本的神经网络的结构和原理有一定的了解，要是还有一些统计推断的知识和基于 python 的机器学习实践就最好了。本文的目的在于阐明不同领域内容之间的联系和逻辑关系，而并不会过于强调基础内容本身。本文的代码实现和流程图参考了文献 2。文献 4 的实现可能更简洁易懂，但拓扑结构上为了讲解还是采取了文献 2 的实现方案。

统计推断视角

问题描述

设想我们现在有一个数据集 X~D，也即若干高维（该维度被称为原始维度）向量 X 共同构成测试数据集 D。如果可以有一个数学模型或者函数，对于每一个原始维度的向量 X 都可以给出一个非负的 P(X)，且对于所有可能的向量，P(X)之和为1，那么很明显 P(X) 可以解释为向量 X 出现的概率。则该数据集全都出现的概率为 \(L＝ \Pi_{X \in D} P(X)\) ，我们的最初目的就是寻找这样一个函数 P(X)，使得可能性 \(L\) 最大。因为我们倾向于认为数据集 D 是自然产生的，那么使其可能性最大的函数最可能是真实的关于原始维度向量产生概率的描述。

为了构造 X 的分布模型，我们引入低维（维度称为隐变量维度）向量隐变量 z，并且认为 X 出现的概率依赖于 z 的值，也就是我们有条件概率公式:

\[P(X) = \sum_{z} P(X\vert z)P(z).\]

现在待求的 X 的概率，已经转化为了在给定 z 下 X 出现的条件概率和隐变量产生的概率的乘积。本文无必要时不区分离散和连续的随机变量分布，我默认读者将 \(\sum\) 等价为 \(\int\) 这件事是明显而自然的。

VAE 的做法在于指定隐变量 \(z\sim N(\vec{0},I)\) 的标准高斯分布，需要注意这里是高维的高斯分布，因此期望 0 是一个向量，而协方差矩阵是单位矩阵。这样做的原因在于 z 本来就是我们假想出来描述 X 可能的概率分布的，因此可以随意指定，但当 z 的分布确定时，\(P(X\vert z)\)就被确定下来而无法随意指定的。设想我们构造了一个依赖参数集 \(\theta\) 的函数 \(f_\theta(X,z)\) 来模拟条件概率\(P(X\vert z)\)的行为，并且通过最大化 \(L\) 来选取最优的参数集 \(\theta\)，这依旧是不可行的，因为对于 z 的求和需要遍及隐变量维度空间的所有向量，而这一求和收敛需要求和的向量 z 的个数是指数增加的，因此实践中并不可行。

优化目标

下面我们根据 K-L 散度的定义，来推导出 VAE 最核心的公式。KL 散度描述了两个随机变量分布之间的相似程度，需要注意的是 KL 散度并不是等价关系，理解成是后一个分布有多像前一个分布更好点。其定义为:

\[D(G(y)\vert \vert H(y)) = \sum_{y} G(y)\ln\frac{G(y)}{H(y)}=E_{y\sim G}(\ln G(y)-\ln H(y)).\]

如果两个分布几乎处处相同，该散度为0，否则该散度恒大于0（散度非负性的证明参考这里）。我们现在来考察一个新的分布函数 \(Q(z\vert X)\) 和 \(P(z\vert X)\) 之间的K-L散度。这一做法的直觉是我们希望用一个构造的分布Q来描述 z 的行为，Q(z) 概率较大表示对应 z 更可能产生指定的 X。而这种用 Q 生成的 z 的可能空间要比原始的需要求和的 z 空间小很多，从隐变量维度全空间求和 \(\sum_z\) 到Q分布较可能状态求和 \(\sum_{z\sim Q}\)，从而使我们可以以较小的计算代价取样估算概率 \(L\)。很自然的，由于 Q 的目的是生成更可能生成目标 X 的 z，我们希望 Q 除了依赖于参数集 \(\phi\) 之外，也依赖目标 X 向量，因此将其定义为 \(Q_\phi(z\vert X)\) 。实践中，我们通常设定 \(Q_\phi(z\vert X)\sim N(\mu_\phi(X),\sigma_\phi(X))\)。这里的协方差矩阵 \(\sigma(X)\) 是对角阵。将 \(P(z\vert X)=\frac{P(X\vert z)P(z)}{P(X)}\) 的贝叶斯公式代入散度（不熟悉贝叶斯定理的请参考这里），化简后我们有:

\[D(Q(z\vert X)\vert \vert P(z\vert X))=E_{z\sim Q}(\ln Q(z\vert X)-\ln P(X\vert z) -\ln P(z))+\ln P(x).\]

注意到求和只与 z 有关， \(P(X)\) 可以被提出均值外（为了便于理解，可以将上式的 X 理解为一个固定的常量），均值内的一三项恰好又可以约化为另一个 K-L 散度的表达式，因此我们有以下 VAE 的核心公式：

\[ELBO(X)=\ln P(X)-D(Q(z\vert X)\vert \vert P(z\vert X))=E_{z\sim Q}(\ln P(X\vert z))-D(Q(z\vert X)\vert \vert P(z)).\]

该公式描述的是对于某个向量 X 的目标函数，等号左边是我们的希望最大化的优化目标（数据集最终的优化目标是\(\sum_{x\in D}ELBO(X)\)）：我们希望最大化 X 出现的概率（第一项），同时使得 \(Q(z\vert X)\) 和 \(P(z\vert X)\) 的分布更加接近（第二项散度更小）。而这一目标可以严格的转化为等号右边，下面我们将看到等号右边的部分是可以计算的。事实上，我们还是有所牺牲，我们只是单纯的想最大化 \(P(X)\)，但等号左边的散度项使得我们无法实现这一点，不过同时我们又获得了额外的好处，通过调参数最大化 ELBO，我们得到了一个 \(Q(z\vert X)\) 函数，并且可以用它来模拟 \(P(z\vert X)\)。但为了计算的可行性，我们最终把这两件事混在了一起，某种程度上，我们很难断言究竟，最大化\(P(x)\)和模拟\(P(z\vert X)\)这两件事单独做到了多好。在某些特殊情况，最大化 ELBO 可以使得该散度为0且真的最大化 P(x) 的存在性得到了证明，具体可以参见参考文献 1 的 2.4.1 和附录 A。

优化计算

观察 ELBO 右边的部分，也就是我们实践中用来计算最优化问题的部分。第一项 \(P_\theta(X\vert z)\) 通常我们也会用复杂依赖参数\(\theta\)的某种分布来模拟。这样 \(\ln P(X\vert z)\) 就可以直接用 \(P_\theta\) 算出，而对于 \(z\sim Q\) 的求期望则可以用多项式数量级的取样求和来代替，实践中通常采取随机梯度下降，多次训练，每次只按概率取出一个隐变量 z 来计算 \(P(X\vert z)\)。

对于第二项散度，两个分布一个是标准分布，另一个也是高斯分布\(Q_\phi(z\vert X)\sim N(\mu_\phi(X),\sigma_\phi(X))\)，两个高斯分布之间的K-L散度很容易直接算出积分求得（具体推导参考这里），

\[D(Q(z\vert X)\vert \vert P(z))=\frac{1}{2}(\mathrm{tr} \sigma+\mu^T\mu-k-\ln \det\sigma),\]

其中 k 指的是隐变量空间维度。由此只需构建 \(\mu_\phi(X),\sigma_\phi(X)\) 两个函数，即可实现 \(Q(z\vert X)\)的分布计算，并得出 ELBO 第二项的具体解析数值。

总结统计推断的部分，为了实现一个隐变量 z 决定变量 X 的模型，我们需要构造两个依赖参数组 \(\phi\) 函数 \(\mu_\phi(X),\sigma_\phi(X)\) 生成分布参数来实现 \(Q(z\vert X)\) 的多维高斯分布，再构造依赖参数组 \(\theta\) 的函数（组）来生成某种合适的分布的参数来实现分布 \(P_\theta(X\vert z)\) 模拟分布 \(P(X\vert z)\)，之后根据这两个分布取样，来计算并最大化 \(\sum_{x\in D}ELBO(X)\)，从而找到最优的参数组 \(\phi,\theta\)，由此得到\(P(X\vert z)\sim P_\theta(X\vert z), P(z\vert X)\sim Q_\phi(z\vert X)\)的近似，这两个函数对于 X 和 z 的相互转化正好对应于解码器和编码器的概念。

神经网络视角

数据预处理

下面我们从神经网络的搭建出发，并结合对 MNIST 手写数字集进行 VAE 建模的 Keras 实例，来重新审视 VAE 在做什么，又是怎么和上面这些统计推断理论联系在一起的。

import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import norm

from keras import backend as K
from keras.layers import Input, Dense, Lambda, Layer, Add, Multiply
from keras.models import Model, Sequential
from keras.datasets import mnist

首先，我们导入并了解一下 MNIST 数据集。

(x_train, y_train), (x_test, y_test) = mnist.load_data()

MNIST 数据集由60000条训练数据和10000条测试数据组成。每条数据 x 都是\(28*28\)像素的内容为手写数字灰度图片（一个\(28*28\)的矩阵，每个元素的取值从0到255，代表图片每个像素点的灰度，大部分矩阵元素为0，代表手写图片的背景）。y 对应该图片代表的数字，范围是0到9。对于 VAE 的网络来说，有点类似于无监督学习，训练目标是输出接近输入，因此我们实际用不到这些数据集的 label 也即 y 的信息。

为了更好更容易的匹配我们前面关于统计推断的部分，我们首先将所有数据矩阵非0的元素都视为1，也即我们忽视灰度信息，只将手写图片视为完全黑（0）白（1）两色的图片，这一做法其实可能会削弱最终网络的精度，这里只是用来做讲解。此外，我们还需要将二维矩阵的信息转化为一维向量，其实这也并非必要，也是为了和上节内容相匹配。

def transform_input(x_t):
    for image in x_t:
        for index_x,index_y in np.transpose(np.nonzero(image)):
            image[index_x][index_y] = 1
    x_t = x_t.reshape(-1, original_dim)
    return x_t
x_train = transform_input(x_train)
x_test = transform_input(x_test)

至此，我们将全部60000+10000组数据，转换为生活在784维线性空间的向量，这向量就是 X，60000向量 X 构成了数据集 D。后文我们还将看到，该网络的隐变量层的维度是2，这样的好处是方便对隐变量数据做可视化，但实际上这么低维度的隐变量损失的信息太多，最后训练的效果不是最优的，仅方便演示。我们将数据集，隐变量和可能用到的隐藏层的维度定义如下。

original_dim = 784
intermediate_dim = 256
latent_dim = 2

构建编码器

编码器负责将输入的某个向量 X 转换为一个随机分布 \(z\sim Q(z\vert X)\)。因为我们总是假设 Q 是一个多维的高斯分布，具体的我们需要用神经网络生成多维高斯分布需要的期望和协方差两个参数即可（输入为 X，输出为 \(\mu_\phi(X),\sigma_\phi(X)\)，\(\phi\)是神经网络包含的参数）。背后的原理是一个预先指定类型的分布在几个分布有关的参数确定时，就唯一确定了。值得注意的是，我们其实有另一种处理编码器的思路，即对于每个数据 X，都直接寻找对应的 \(\mu,\sigma\) 使得损失函数最小，也即直接用 \(\mu,\sigma\) 作为参数实现最优化。这样对于每一个 X 都需要重新训练，来寻找对应该 X 对应的最优分布参数 \(\mu,\sigma\)，这显然是无法接受的。因此我们这里采用普适参数确定的神经网络作为函数，通过输入 X 直接获得输出的分布参数，我们采用的这种学习普适的推断网络的做法被称为 amortized inference。实现代码如下，我们添加了一层隐藏层增加模拟能力。

# x: InputLayer
x = Input(shape=(original_dim,))
# hidden_enc: Dense
h = Dense(intermediate_dim, activation='relu')(x)
# mu: Dense
z_mu = Dense(latent_dim)(h)
# log_var: Dense
z_log_var = Dense(latent_dim)(h)

代码实现的网络拓扑参见下图最上面三层，我们将要用神经网络实现的 VAE 的整体结构均在此图之中。各层将在后文依次实现。

网络结构与统计推断的类比

在进一步构造其他层之前，我们先从整体上对上图的神经网络拓扑结构进行分析，并匹配上节讨论的统计推断的相关概念。最初的给定数据 X，生成隐变量 z 的高斯分布的编码器部分，在上小节已经阐述并实现。下一步则为按照 z 的分布概率选出一个具体的 z 向量作为后续解码器部分的输入向量。这一步相当于按照分布采样，对于大量数据的反复处理就相当于实现了 \(\sum_{z\sim Q}\) 这一过程。如果使得反向传播算法，和梯度计算的链式法则成立，我们需要将对 z 采样这一过程从神经网络的中间层剥离出去，此处利用的重参数化的技巧，我们具体构造时再详细叙述。而同时我们又实现了了一个计算 K-L 散度的中间层，来叠加到最后的损失函数上。

总之我们通过重参数化技巧，从 z 的高斯分布采样一个具体的 z 向量，之后 z 将被输入到解码器的神经网络中，从而生成一个输出向量。在最广泛的意义上，解码器的输出是某个适合该问题指定类型随机变量分布的几个决定参数组（和编码器类似）。因为解码器实际上就是在实现 \(P(X\vert z)\)，需要再次注意，这里的 \(P(X\vert z)\)是一个随机变量分布，因此输出目标的并不是 X 本身！并不是 X 本身！并不是 X 本身！这一点在从神经网络出发讲解 VAE 时经常被混淆。严格的来说， VAE 模型完全是基于统计推断的，出发点并不是所谓的编码器解码器结构，因此这一相似只能是停留在相似层面，从解码器编码器原理出发来简单理解和构建 VAE 也不能说错（有时还是很有效），但是绝对是不严谨的（取决于你的价值观，大可以直接反驳：反正机器学习全都是炼丹术，还谈什么严不严谨。如果持这一观点，那就不需要读下去了，简单将 VAE 理解成一个有特殊正规化项的普通解码器完全可以解决实际问题了）。广义来看，VAE 的编码器解码器并不对称，编码器：X 本身 \(\rightarrow\) 已知 X 条件下，z 的高斯分布\(Q(z\vert X)\)（通过生成多维高斯分布参数的形式确定）；取样器：z 的条件分布参数\(\rightarrow\)一个具体的 z 向量，通过重参数化的技巧，按\(Q(z\vert X)\)的分布采样一个 z；解码器：该具体的 z 向量 \(\rightarrow\)已知z的条件下，X的分布 \(P(X\vert z)\)（通常直接指定该分布的类型，如波努力分布，高斯分布等。因此生成的实际上也是一系列决定该分布的参数）。最后的损失函数就是上节提及的 ELBO 的相反数，因此最小化该目标，即一定程度上（相差一个被相信会接近零的 K-L 散度项）最大化了数据集出现的概率 \(L\)。需要注意，损失函数第一项是 \(\frac{1}{N}\sum^{n=N}_{z_n\sim Q}P(X\vert z_n)\)。并不天然是编码器输入 X 和解码器输出的交叉熵。损失函数的这一项并不天然是在衡量输入与最后输出的差异！这段话是 VAE 结构的核心，也是有效的建立起统计推断和神经网络两者之间联系的看法，而这一看法在以前的文献中几乎都没有阐述的足够清晰。如果没有完全懂这一段，请再看一遍，或继续看下面段落，关于此段落结合具体实例 MNIST 识别的解释。

现在我们结合 MNIST 的具体例子，来看上面这段话的含义，并且来分析，为何最后的目的输出似乎就是 X 本身，以及为何大家使用的损失函数就是包含的输入输出的交叉熵项。一定要注意，以上两点是该例子的特殊推论，并不代表 VAE 天生的目的输出就是输入，或者应该用交叉熵来评估损失函数，代替概率对数项（当然大多数情况下，大家还是这么做了，即使不严格，也无法像该例子一样等价性得到证明）。

在 MNIST 的例子里，数据集中的 X 向量是784维的向量，且每一个元素只能取0或1。我们对数据本来从0到255的数据的预处理是该问题的关键。比起通常的做法直接将元素全部除以255，这里我们将所有非零元素直接都设成1。之后通过编码器生成隐变量维度的均值向量和协方差向量的对角项向量（我们的例子里均为2维）。之后按这些参数确定的多维高斯分布的概率采样一个具体的2维的 z 向量作为解码器的输入。解码器神经网络最后输出一个784维的向量且每个元素都是介于01之间的实数（可通过激活函数设置为sigmoid实现）。注意到我们的X，元素只能两点取值0或1。而这些有实数值的输出向量（暂时称为dout），不是 X 中的一员。回忆解码器的输出应该是某种指定分布的参数，我们现在开始解释 dout 向量的意义。dout 的每个元素，都表示该元素上的一个两点分布。比如 \(dout[0]=0.7\)，就表示预测X向量的第一个元素是1的概率为0.7而是0的概率为0.3。也即输出给的是\(P(X[0]=1\vert z)=0.7\)，也就是输出的落脚点还是分布，是确定分布的参数，这里就是多重独立的两点分布的各个参数，而不是输入 X！还记得要算的损失函数的第一项么，

\[\ln(P(X\vert z))=\ln\Pi^{783} _{i=0}P(X[i]=X[i]\vert z)=\sum^{783}_{i=0} X[i]\ln dout[i]+(1-X[i])\ln(1-dout[i])\]

最后一个等号只需考虑 \(X[i]\)只有等于1或0两种情况，则是显然的。比如对于 \(X[i]=0\)，\(\ln P(X[i]\vert z)=ln(1-dout[i])\)。于是我们发现在我们构造的特殊模型里，恰好解码器输出分布在输入 z 的条件概率的对数就是输入输出向量之间的交叉熵公式。一定严格的意义上，我们损失函数使用常用的交叉熵在这里是巧合而不是本来的要求。根据统计推断，最基本的损失函数的量是条件概率对数。而对于输出的 dout 除了最严谨的概率分布参数这种解释外，其实也可以直接转化为灰度图像，不是原始的黑白两色图片，多了灰的梯度色彩丰富了而已，因此很多情况下，解码器分布参数的输出 dout 也可以某种程度上理解为是输入 X 的同类。

所以使用交叉熵做为损失函数的一项以及将解码器输出理解为是 X 的类似物，均只在特定情形下严格成立，当然绝大多数情形，没人考量以上等价性的严格程度也在随便使用，这也是大部分关于 VAE 困惑，统计推断方向和神经网络方向的看法无法协调自洽起来的根源。

构建损失函数

VAE 神经网络的损失函数就是统计推断里得出的 ELBO 的相反数，因此最小化该损失函数即可最优化参数。我们当然可以直接自定义一个损失函数来包含 ELBO 中概率对数项（该问题中恰好对应输入输出交叉熵）和涉及中间层参数的 K-L 散度项，不过我们这里通过一个中间层来记录 K-L 散度项并将其加在最后的损失函数上，这样做使我们更方便的修改散度项的内容，扩展性好一些。因此我们需要定义一个自定义损失函数记录交叉熵部分，并通过一个额外的层来将 K-L 散度部分添加到损失函数上。

# loss function
def nll(y_true, y_pred):
    return K.sum(K.binary_crossentropy(y_true, y_pred), axis=-1)
   
# customized layer: kl:KLDivergenceLayer
class KLDivergenceLayer(Layer):
    def __init__(self, *args, **kwargs):
        self.is_placeholder = True
        super(KLDivergenceLayer, self).__init__(*args, **kwargs)
    def call(self, inputs):
        mu, log_var = inputs
        kl_batch = - .5 * K.sum(1 + log_var -
                                K.square(mu) -
                                K.exp(log_var), axis=-1)
        self.add_loss(K.mean(kl_batch), inputs=inputs)
        return inputs
# kl:KLDivergenceLayer  
z_mu, z_log_var = KLDivergenceLayer()([z_mu, z_log_var])

注意到这里，我们将本来损失函数的第一项 \(E_{x\in D}E_{z\sim Q}P(X\vert z)\) ，我们采取了蒙特卡洛取样的方式估算该项，每个数据点 X 只取一个 \(P(X\vert z)\) 来对期望进行估计。也就是说，每次蒙卡取样估算条件概率均值的取样总数为 batch size。这么小的取样数就已经可以获得不错的结果。关于调大计算概率期望的蒙卡样本数的实现，可以参考这里。

构建采样器

首先注意我们编码器部分生成的是协方差矩阵对角项向量的对数，我们需要通过一个 lambda 函数层将其还原为协方差对角向量（做一次指数计算）。

# sigma: Lambda
z_sigma = Lambda(lambda t: K.exp(.5*t))(z_log_var)

这时我们就需要用重参数化的技巧，将从随机分取样这一过程从网络的链路里分离出来，使得梯度下降的链式法则可以工作。如果取样层直接在网络的路径上，反向传播就会被阻断。因此我们输入一个标准正态分布采样点，并通过一些参数将其转化为 z 的采样，这样采样的过程作为输入独立出了 VAE 的训练网络，不会对我们的反向传播算法产生影响。

epsilon_std = 1.0
# eps: InputLayer
eps = Input(tensor=K.random_normal(stddev=epsilon_std,
                                   shape=(K.shape(x)[0], latent_dim)))
# z_eps: Multiply
z_eps = Multiply()([z_sigma, eps])
# z: Add
z = Add()([z_mu, z_eps])

需要注意这里的 Input 层，使用了 tensor 参数，适用于常数或随机变量的输入层。这种 Input 层只需在模型编译中指定输入，但不需要在模型训练时给定输入数据。

构建解码器

解码器很简单，给定两维向量输入 z，输出 784 维的向量即可，为了使的每个元素的数字都处在0至1之间（作为两点分布的参数），最后加一个 sigmoid 的激活函数即可。同时尽量使得解码器部分和编码器部分保持一定的结构上的对称性也许会对学习的有效性有一定帮助。

decoder = Sequential([
    Dense(intermediate_dim, input_dim=latent_dim, activation='relu'), #hidden_dec: Dense
    Dense(original_dim, activation='sigmoid') #x_pred:Dense
])
x_pred = decoder(z)

模型编译与训练

将以上函数式实现的各层连接成一个模型 vae，编译并用 MNIST 数据进行训练（仅为演示，训练的 epochs 并不大）。

batch_size = 200
epochs = 30

vae = Model(inputs=[x, eps], outputs=x_pred)
vae.compile(optimizer='adam', loss=nll)
vae.fit(x_train,
        x_train,
        shuffle=True,
        epochs=epochs,
        batch_size=batch_size,
        validation_data=(x_test, x_test))

结果可以进行一些简单的可视化，

# display a 2D plot of the digit classes in the latent space
z_test = encoder.predict(x_test, batch_size=batch_size)
plt.figure(figsize=(6, 6))
plt.scatter(z_test[:, 0], z_test[:, 1], c=y_test,
            alpha=.4, s=3**2, cmap='viridis')
plt.colorbar()
plt.show()

# display a 2D manifold of the digits
n = 15  
digit_size = 28

u_grid = np.dstack(np.meshgrid(np.linspace(0.05, 0.95, n),
                               np.linspace(0.05, 0.95, n)))
z_grid = norm.ppf(u_grid)
x_decoded = decoder.predict(z_grid.reshape(n*n, 2))
x_decoded = x_decoded.reshape(n, n, digit_size, digit_size)

plt.figure(figsize=(10, 10))
plt.imshow(np.block(list(map(list, x_decoded))), cmap='gray')
plt.show()

得到的手写数字图片在2维隐变量空间的可视化为。

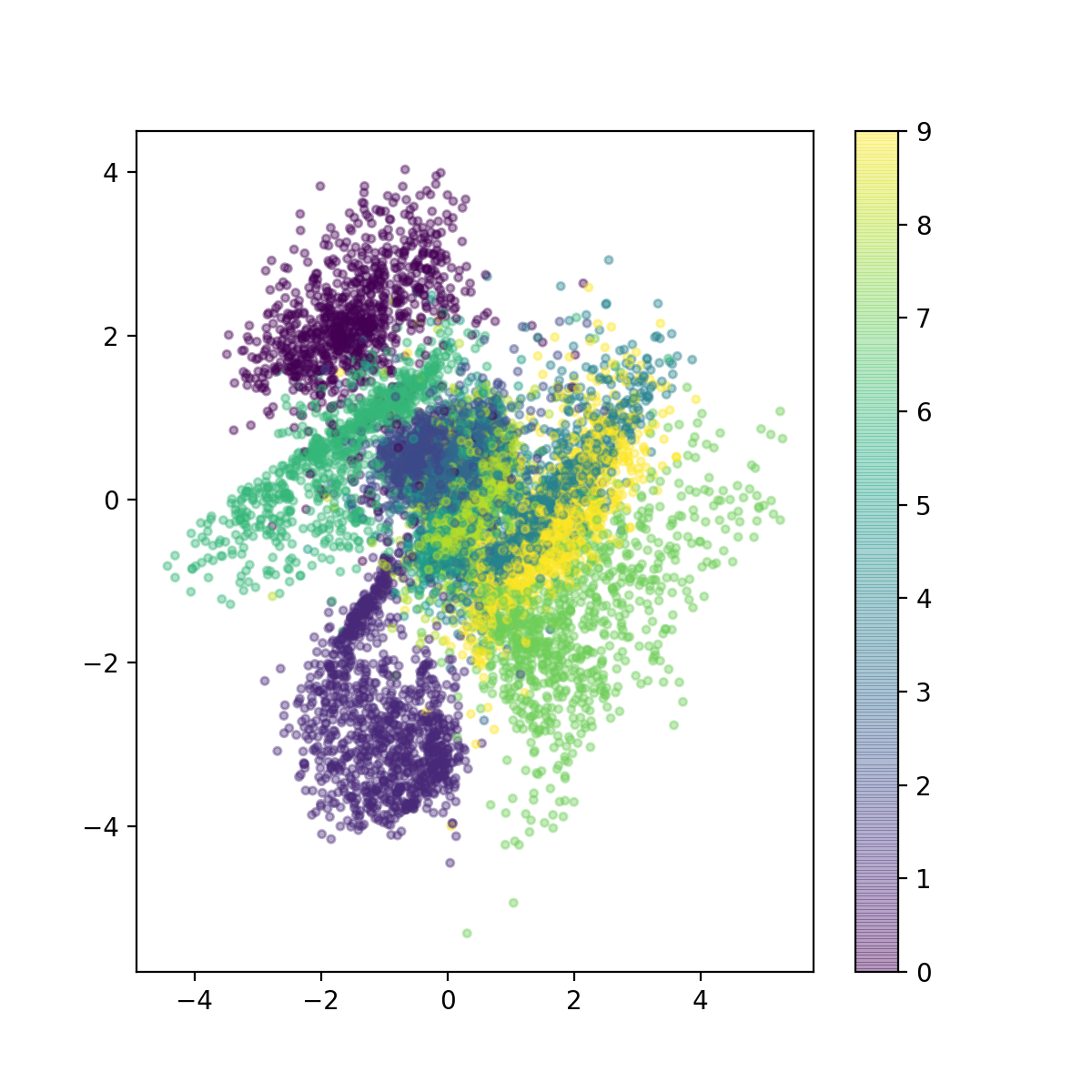
可以看到，不同数字的图片在隐变量空间发生了分离，但是有些数字的样本点非常接近，而这些数字确实图像上比较相似。比如9和7。可以想象如果隐变量空间维度更高，将会获得图片的更多特征，而数字之间也将分的更开，对应的识别效果将更好。根据参考文献1，隐变量空间维度从4到1000，效果都很好，也就是 VAE 对隐变量维度并不太敏感。

而通过隐变量空间的均匀取点作为解码器的输入来生成新的数字图片如下。

可以看出这样生成的数字，边界比较模糊，这也是 VAE 网络的特点，由于随机分布采点，总是倾向生成比较模糊连续的图片，因为其隐变量空间根本就是连续的。这一点和边界比较锐利的 GAN 方案相反。可以看到生成的数字里有很多四不像类似不同数字间的过渡，这一点从上面隐变量空间不同数字的分布及其相互交迭也可以得到解释。如果希望得到更清晰更有效的数字图像生成方案，可以考虑使用条件变分自动编码器（CVAE），输入引入 label 形成一定程度的监督学习，具体实现和原理参见这里。

统计推断推广分析

我们延续平行类比神经网络和统计推断的思路，将只具有01两个值的输入 X 推广到具有0-255灰度的图片 X 的情形。首先我们将原始的 MNIST 图片向量除以255，归化成每个元素都在01之间的784维向量 X。而对于解码器的输出 dout，依旧也是一个 784 维的，元素在01之间的实数向量。这时根据我们统计推断的精神，如何来求损失函数，又如何理解输入输出这两个形式完全一样的向量，一个是图片本身，另一个是某种概率分布的参数呢？我们延续对比统计推断和神经网络的思路来分析这个输入变量不只有0或1两个取值的问题。以下的分析比较激进，我也没见其他人提及过，可能的错误欢迎指出。

记住我们的出发点是统计推断，因此解码器生成的一定是某个分布 \(P(X\vert z)\)，实践上一般指定某种类型的分布，通过解码器网络生成可以唯一确定分布的参数，这些参数实践上通常是和输入向量同维度的参数向量。这也比较好理解，相当于我们倾向于生成一些 X 分量的独立分布 \(P(X[i]\vert z)\) 来模拟整个 X 向量的分布，这里我们分别做了 X 的实际条件分布可以用我们指定的类型分布来逼近和 X 各分量的分布相互独立两个近似。后者近似实际可以放弃，只要你不嫌麻烦，选择生成关于 X 整体的高维分布处理，这里不详细讨论这种情况。

最广义的讲，解码器生成参数组 \(\vec{p'}\)所确定的概率分布，与原始的输入 X，（由于我们总是可以把 X 归一化成每个分量处在01之间的实数，我们可以把这种对应的输入向量 X 记为 \(\vec{p}\)，p 和 X 在下文完全是同义词！），给出了 \(p\) 在 \(p'\) 确定的分布下的概率，我们记为 \(f(p,p')\)。既然是概率，需要满足归一化限制，也即 \(\int dp f(p,p')=1\)。不过注意到我们总可以将这一函数写为 \(f(p,p')=g(p)h(p,p')\)，而 \(g(p)\) 部分是固定的，调参数改变 \(p'\) 的值不会影响这一部分，也即:

\[\sum \ln P(X\vert z)=\sum \ln f(p,p')=\sum\ln h(p,p')+\underline{\sum\ln g(p)}.\]

下划线部分做最优化是是定值可以直接省略，因此我们设定的解码器输出的分布类型 \(h(p,p')\) 只要是函数即可，没有任何限制，归一化问题会自动满足而不需考虑。考虑到大多数时候我们希望用 VAE 做的事情是生成类似输入 X 的东西，最后我们需要加一个函数 \(d(p')=X\) 将编码器输出的分布特征参数转化为类似输入的向量。如果基于 VAE 统计推断的原教义，我们要训练的损失函数是 \(p,p'\) 之间的部分，因此最后 \(d\) 函数这层的网络是无法训练的（输出没有约束和最优化的过程），所以我们通常都是找一个随手写下的 \(d\) 函数层来完成最后的将编码器输出转化为输入类似向量的过程。只不过在大多数情况下，既然输入是元素介于01之间的向量，而编码器输出的分布特征参数向量也是，同时这些特征参数又在一定程度上代表了分布的最可几或是期望等信息时，我们倾向于最后的 \(d＝I\)，也即加一个恒等函数层来将分布参数转化为类似输入的东西。一个恒等层等于什么都没有，这也是理解上可能的困惑来源。为了统计推断更好的匹配神经网络部分，还是加上这层输出转换层进行思考为宜。

现在看几个具体的指定 \(P(X[i]\vert z)\) 分布类型的例子。为了方便，我们直接将输入 X 的每个元素看成连续的实数（实际上在 MNIST 例子里，元素只有 256 个离散的取值。）在连续分布的情况下，我们可以讲前面所说的所有概率换为概率密度，为了叙述方便，我将仍采用概率符号，只需读者记得连续情形这指的是概率密度即可。

第一个例子，我们指定最后的输出是（有截断的）高斯分布，即 \(P(X[i]\vert z)\sim N(\mu=p'[i]，\sigma^2)\)，也即 \(h(p[i],p'[i])=Exp(-\frac{1}{2\sigma^2}(p[i]-p'[i])^2)\)。损失函数 K-L 散度的部分总是可以解析计算，我们还是关注条件概率对数的部分。

\[\ln P(X\vert z)=\sum _i\ln P(X[i]\vert z)=\sum_i \ln h(p[i],p'[i])=\sum_i -\frac{1}{2\sigma^2} (p[i]-p'[i])^2.\]

有没有很熟悉，如果我们使用高斯分布作为解码器的输出，那么损失函数的第一项将是输入和输出的平方损失而非交叉熵损失。这就是反复强调 VAE 的损失函数绝不是天生是交叉熵的原因。

第二个例子，我们取分布为

\[h(p[i],p'[i])=\frac{1}{\Gamma(1+p[i])\Gamma(2-p[i])}p[i]'^{p[i]}(1-p'[i])^{(1-p[i])}.\]

事实上如果注意到 Gamma 函数和阶乘的关系，这一分布很类似二项分布，只不过是从1个里取出不到1个的概率。注意到分布的因子只包含 \(p\) ，因此计算损失函数时是定值而可以省略，对应的损失函数第一项则为

\[\ln P(X\vert z)=\sum_i p[i]\ln p'[i] +(1-p[i])\ln (1-p'[i]).\]

这一损失正好是交叉熵的形式。因此 VAE 的损失函数究竟怎么表示，从统计推断出发，这一问题完全取决于你选取的解码器输出的分布是哪种类型的，这一分布的不同就会导致最后损失函数的不同。

广义的，损失函数这项的形式为

\[\ln P(X\vert z) = \ln h(p,p') =\sum_i\ln h (p[i],p'[i]).\]

最后一个等号只在输出的分布各项独立时成立，也是我们一直在用的情形。基于前边我们说的 h 函数可以取任意形式的结论，VAE 的损失函数可以长成任意样子，具有任意系数（也即和K-L散度项的权重比例可以随意调整）！你肯定对这个结论惊呆了，前边的平方和对数误差的形式还可以接受，怎么可能损失函数随便乱取能使得输出和输入接近呢？没错，随便取当然不会使输入和输出接近，你忘了输出只不过是分布的特征参数而并非以输入为目标了么。既然我们任意改变了指定的输出的分布类型，那么自然训练结果输出和输入可以大相径庭。这才是 \(d\) 函数层存在的意义啊！只有 d 输出的东西才像输入，而不是解码器的输出。只不过我们选取比较典型的分布，决定分布的特征参数很大程度上代表了分布的最可几值，使得我们可以将这些参数作为最终输出，也就是将 d 层取为了恒等层而已。对于更奇怪的分布，损失函数长得可能前所未见，但这并不影响生成最后的图片，只是需要 d 层函数按这个奇怪的分布算个期望或最可几值即可，这一输出就会重新像图片。

因此为了从统计推断理解 VAE，其整体结构应为：（斜体为输入输出值，加粗的为神经网络层或者理解为函数）

原始向量 X（也记为p）—> 编码器 —> 高斯分布(通过输出期望\(\mu\)方差\(\sigma\)两组参数确定) —> 取样器 —> 按高斯分布采样的向量 z —> 解码器 —> 某种指定类型（函数h形式）的分布（通过输出特征参数 p’ 确定） —> 转换器（函数层 \(d\)） —> 输出向量 \(X'\) （目标是尽可能接近输入 X）

其中转换器将\(p'\)转换为\(X'\)这一步对于 VAE 的理解至为关键，逻辑上不可或缺（实践上几乎总缺）。

Reference

Tutorial on VAE: arxiv
Implementation on VAE in Keras: Louis Tiao’s blog
What is a VAE: Jaan’s post
VAE: intuition and implementation: Kristiadi’s blog
Building aotoencoder in keras: The Keras Blog
Relevant wikipedia items

EOF